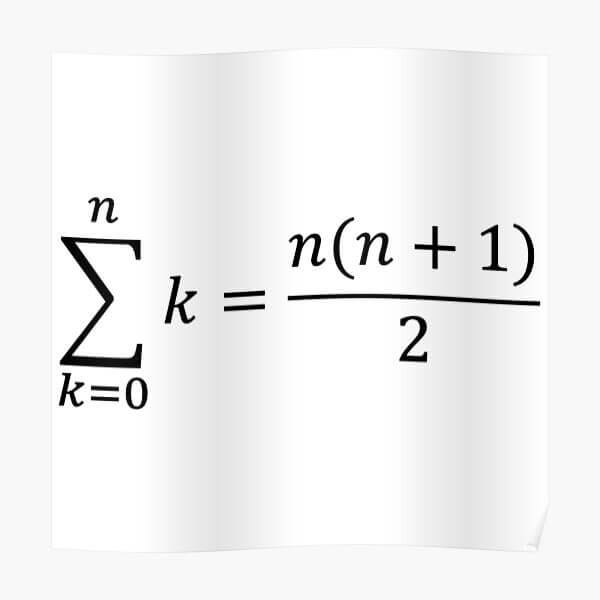
Multiplicación de números naturales
Este capítulo marca la transición de lo abstracto a lo concreto. Considerar el universo matemático en términos de conjuntos, relaciones y funciones nos proporciona formas útiles de pensar en los objetos y estructuras matemáticas y en las relaciones entre ellos. Sin embargo, en algún momento tenemos que empezar a pensar en objetos y estructuras matemáticas concretas, y los números naturales son un buen punto de partida. El matemático del siglo XIX Leopold Kronecker proclamó en una ocasión que “Dios creó los números enteros; todo lo demás es obra del hombre”. Con esto quería decir que los números naturales (y los enteros, de los que también hablaremos a continuación) son un componente fundamental del universo matemático, y que a partir de ellos se pueden construir muchos otros objetos y estructuras de interés.
En este capítulo estudiaremos los números naturales y los principios básicos que los rigen. En el capítulo 18 veremos que incluso las operaciones básicas, como la suma y la multiplicación, pueden definirse utilizando los medios aquí descritos, y sus propiedades se derivan de estos principios básicos. Sin embargo, nuestra presentación en este capítulo seguirá siendo informal. En el capítulo 19, veremos cómo se aplican estos principios en la teoría de los números, una de las ramas más antiguas y venerables de las matemáticas.
Suma de cuadrados de n números naturales
La fórmula de la suma de números naturales se obtiene utilizando la fórmula de la progresión aritmética en la que la diferencia común entre el número anterior y el posterior es 1. Los números naturales también se llaman números de conteo y comienzan desde el número 1 hasta el infinito, como 1,2,3,4,5,6,7, etc. Conozcamos la suma de n números naturales, cómo se obtiene la fórmula y resolvamos algunos ejemplos.
La suma de n números naturales puede definirse como una forma de progresión aritmética en la que la suma de n términos se ordena en una secuencia en la que el primer término es 1, siendo n el número de términos junto con el término n. La suma de n números naturales se representa como [n(n+1)]/2. Los números naturales son los números que empiezan por el 1 y terminan en el infinito. Los números naturales incluyen números enteros en ellos excepto el número 0.
Suma de todos los números naturales
Esto es una simple progresión aritmética. Una suma de números naturales del 1 al n. La respuesta es n(n+1)/2. Al menos, esto es lo que nos han enseñado durante toda nuestra escolaridad. Así que, si ‘n’ tendiera a infinito, la suma debería tender a infinito. ¿No es así? ¡¡Error!! Sí, los matemáticos dicen que no. ¿Hay algún misterio oculto detrás de esto?
¿Cómo un doble “no”? ¿Nos están tomando el pelo los teóricos de los números? ¿Es esto una pseudociencia? No puede ser negativo. ¡Nunca negativo! Así que vamos a dejar esta suma que parece demasiado difícil. Permítanme escribir algo más. Siempre veneré a Ramanujan como uno de los más grandes matemáticos de todos los tiempos. El puro genio de Ramanujan en la teoría de números siempre me fascinó. El gran hombre a menudo ignoraba las pruebas para muchas de las derivaciones. Es así; un genio mira un problema, el camino parece obvio, así que se salta los pasos, llega a la solución, pero los matemáticos siguen dándole vueltas a las conjeturas de la izquierda. ¡¡¡Así que sí Ramanujan también hizo matemáticas interesantes en el campo de la suma infinita y la siguiente afirmación me choca!!! El método de Ramanujan para la suma de números, apunta al hecho ‘S’= -1/12. ¿Ramanujan? ¿No estudió la fórmula básica n(n+1)/2? ¿O esas cosas de las series divergentes? Pero otro eminente matemático se dedicó a demostrar que ‘S’=-1/12. Este fue “Riemann”. Sí, es bien conocido por las funciones zeta y reputado como uno de los mejores matemáticos de los últimos tiempos; pero ¿1/12?
¿Qué es adición de números naturales? online
Este artículo contiene pruebas matemáticas de algunas propiedades de la suma de los números naturales: la identidad aditiva, la conmutatividad y la asociatividad. Estas pruebas se utilizan en el artículo Suma de números naturales.
A continuación demostraremos el caso base b = 1, que el 1 conmuta con todo, es decir, para todos los números naturales a, tenemos a + 1 = 1 + a. Lo demostraremos por inducción sobre a (una prueba de inducción dentro de una prueba de inducción). Hemos demostrado que el 0 conmuta con todo, así que en particular, el 0 conmuta con el 1: para a = 0, tenemos 0 + 1 = 1 + 0. Ahora, supongamos que a + 1 = 1 + a. Entonces
Esto completa la inducción sobre a, y así hemos demostrado el caso base b = 1. Ahora, supongamos que para todos los números naturales a, tenemos a + b = b + a. Debemos demostrar que para todos los números naturales a, tenemos a + S(b) = S(b) + a. Tenemos
