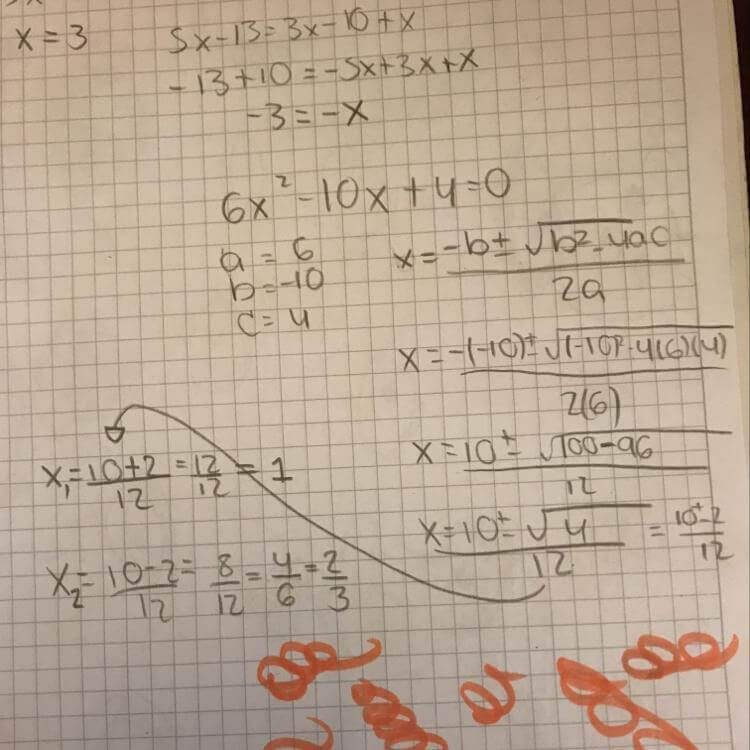
Ejercicios de ecuaciones irracionales
En un ejercicio te piden que uses la regla de Ruffini. Estás a punto de hacerlo, pero te das cuenta de que no sabes ni cómo empezar. Has visto a tu profesor en clase hacerlo varias veces, pero ahora no sabes cómo conozco el método de Ruffini
Para resolver ecuaciones de primer grado usamos un método, para las de segundo grado usamos otro y para resolver las de tercer grado o más, o sea, para ecuaciones de más de dos grados, usamos el método de Ruffini.
Lo que nos queda en la última fila es otra ecuación, pero ahora, el número a la izquierda de 0 tiene grado 0 y es creciente de 1 en 1 a la izquierda. En este caso, tenemos el equivalente a tener esta ecuación:
Esta vez, el número que tenemos que colocar a la izquierda de la línea vertical es el 2 (la a del binomio x-a) y no tenemos que preocuparnos de si tenemos un cero en la última columna o no. El resultado será el resto de la división:
Ecuaciones no racionales
*Nota: Hay otro enfoque que escribe los términos en orden creciente de la potencia de x. Esto tiene cierto atractivo porque así escribimos series de potencias. Tendrás que elegir cuál te conviene.
Las funciones polinómicas (normalmente decimos simplemente “polinomios”) se utilizan para modelar una gran variedad de fenómenos reales. En física y química, en particular, conjuntos especiales de funciones polinómicas con nombre, como los polinomios de Legendre, Laguerre y Hermite (¡menos mal que son franceses!), son la solución de algunos problemas muy importantes.
Es importante que te hagas experto en trazar las gráficas de las funciones polinómicas y encontrar sus ceros (raíces), y que te familiarices con las formas y otras características de sus gráficas.
Puedes comprobarlo tú mismo haciendo una hoja de cálculo rápida. Pon una columna x y rellénala con valores enteros del 1 al 10, luego calcula el valor de cada término (4 columnas más) a medida que x crece. Súmalos y añade el término constante (22) para encontrar el valor del polinomio. El término principal es el que crece más rápidamente. Esto es lo que quiero decir:
Ejercicios de ecuaciones bicadráticas
Un sistema de ecuaciones polinómicas (a veces simplemente un sistema polinómico) es un conjunto de ecuaciones simultáneas f1 = 0, …, fh = 0 donde las fi son polinomios en varias variables, digamos x1, …, xn, sobre algún campo k.
Una solución de un sistema de polinomios es un conjunto de valores para las xis que pertenecen a alguna extensión de campo algebraicamente cerrado K de k, y hacen que todas las ecuaciones sean verdaderas. Cuando k es el campo de los números racionales, generalmente se asume que K es el campo de los números complejos, porque cada solución pertenece a una extensión de campo de k, que es isomorfa a un subcampo de los números complejos.
Este artículo trata de los métodos para resolver, es decir, encontrar todas las soluciones o describirlas. Como estos métodos están diseñados para ser implementados en un ordenador, se hace hincapié en los campos k en los que el cálculo (incluyendo la comprobación de la igualdad) es fácil y eficiente, es decir, el campo de los números racionales y los campos finitos.
La búsqueda de soluciones que pertenezcan a un conjunto específico es un problema que suele ser mucho más difícil, y queda fuera del ámbito de este artículo, excepto para el caso de las soluciones en un campo finito dado. Para el caso de las soluciones cuyos componentes son todos números enteros o racionales, véase Ecuación diofantina.
Ejemplo de polinomio bicadrático
Una nueva panadería ofrece tartas decoradas para fiestas de cumpleaños de niños y otras ocasiones especiales. La panadería quiere que el volumen de una tarta pequeña sea de 351 pulgadas cúbicas. El pastel tiene forma de sólido rectangular. Quieren que la longitud de la tarta sea cuatro pulgadas más larga que la anchura de la tarta y que la altura de la tarta sea un tercio de la anchura. ¿Cuáles deben ser las dimensiones del molde?
Este problema se puede resolver escribiendo una función cúbica y resolviendo una ecuación cúbica para el volumen del pastel. En esta sección, discutiremos una variedad de herramientas para escribir funciones polinómicas y resolver ecuaciones polinómicas.
En la última sección, aprendimos a dividir polinomios. Ahora podemos usar la división de polinomios para evaluar polinomios usando el Teorema del Resto. Si el polinomio se divide por x – k, el resto se puede encontrar rápidamente evaluando la función polinómica en k, es decir, f(k). Veamos la demostración del teorema.
Recordemos que el Algoritmo de la División establece que dado un dividendo polinómico f(x) y un divisor polinómico distinto de cero d(x) donde el grado de d(x) es menor o igual que el grado de f(x), existen polinomios únicos q(x) y r(x) tales que
