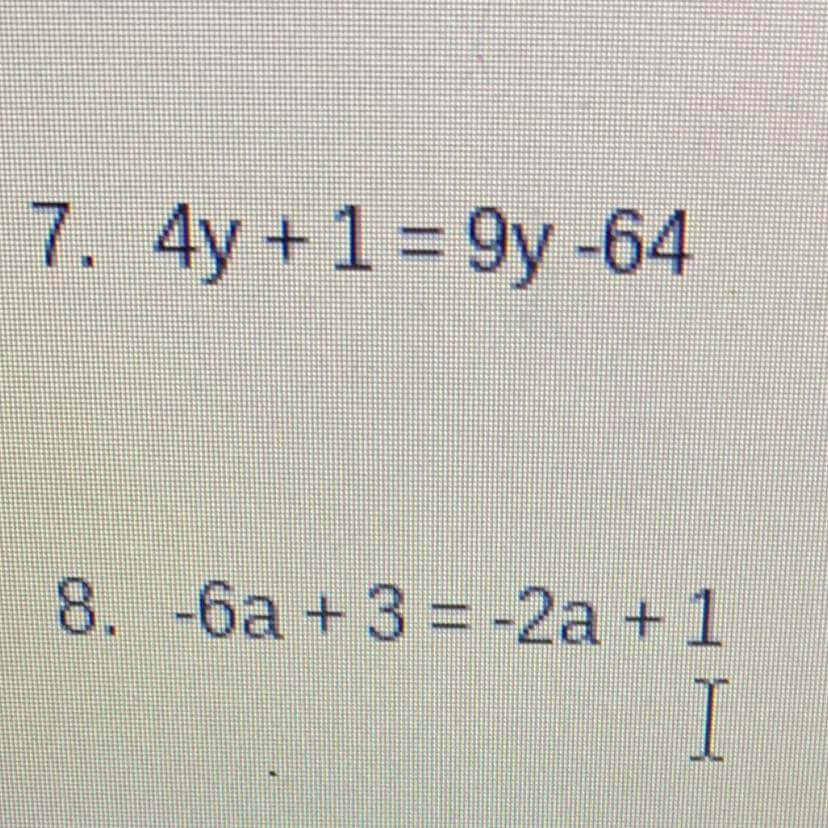
Ejercicios de ecuaciones de primer grado pdf
Este artículo trata sobre las ecuaciones algebraicas de grado dos y sus soluciones. Para la fórmula utilizada para encontrar soluciones a dichas ecuaciones, véase Fórmula cuadrática. Para funciones definidas por polinomios de grado dos, véase Función cuadrática.
término. Los números a, b y c son los coeficientes de la ecuación y pueden distinguirse llamándolos, respectivamente, coeficiente cuadrático, coeficiente lineal y término constante o libre[1].
Los valores de x que satisfacen la ecuación se denominan soluciones de la misma, y raíces o ceros de la expresión en su lado izquierdo. Una ecuación cuadrática tiene como máximo dos soluciones. Si sólo hay una solución, se dice que es una raíz doble. Si todos los coeficientes son números reales, hay dos soluciones reales, o una única raíz doble real, o dos soluciones complejas. Una ecuación cuadrática siempre tiene dos raíces, si se incluyen las raíces complejas; y una raíz doble se cuenta por dos. Una ecuación cuadrática se puede factorizar en una ecuación equivalente
Ejemplos de ecuaciones de primer grado
Las ecuaciones son de primer grado cuando pueden escribirse en la forma ax + b = c, donde x es una variable y a, b y c son constantes conocidas y a ¡a!=0. Discutimos las técnicas para resolver ecuaciones de primer grado en la sección 3.4 y de nuevo en la sección 3.5 al tratar las fórmulas. Además, encontrar las soluciones a las proporciones discutidas en las secciones 6.6 y 6.7 implica resolver ecuaciones de primer grado.
Este tema es uno de los más básicos e importantes para cualquier estudiante principiante de álgebra y se presenta de nuevo aquí para reforzarlo positivamente y como preparación para resolver una variedad de aplicaciones en las secciones 7.3, 7.4 y 7.5.
Hay exactamente una solución para una ecuación de primer grado en una variable. Esta afirmación puede demostrarse por el método de la contradicción. La prueba no se da aquí. Las ecuaciones que tienen más de una solución se discutirán en los capítulos 8, 9 y 10.
Esta última técnica tiene la ventaja de dejar sólo los coeficientes enteros y las constantes. Si hay más de una fracción, entonces cada término debe ser multiplicado por el LCM de los denominadores de las fracciones.
Ecuación de primer grado en dos variables
Este artículo trata sobre las ecuaciones algebraicas de grado dos y sus soluciones. Para la fórmula utilizada para encontrar las soluciones de dichas ecuaciones, véase Fórmula cuadrática. Para funciones definidas por polinomios de grado dos, véase Función cuadrática.
término. Los números a, b y c son los coeficientes de la ecuación y pueden distinguirse llamándolos, respectivamente, coeficiente cuadrático, coeficiente lineal y término constante o libre[1].
Los valores de x que satisfacen la ecuación se denominan soluciones de la misma, y raíces o ceros de la expresión en su lado izquierdo. Una ecuación cuadrática tiene como máximo dos soluciones. Si sólo hay una solución, se dice que es una raíz doble. Si todos los coeficientes son números reales, hay dos soluciones reales, o una única raíz doble real, o dos soluciones complejas. Una ecuación cuadrática siempre tiene dos raíces, si se incluyen las raíces complejas; y una raíz doble se cuenta por dos. Una ecuación cuadrática se puede factorizar en una ecuación equivalente
Ejemplos de ecuaciones de primer grado en una variable
Una ecuación de primer grado es aquella que, reducida a su forma más simple, contiene la letra o letras desconocidas elevadas sólo a la primera potencia. Así, las ecuaciones 5x -7=18 y 3x + 5x -2 = 34 -x son ecuaciones de primer grado. La ecuación 2×2 + 7 x -3x -2×2 = 28, tal como está escrita, no parece una ecuación de primer grado, ya que contiene la incógnita elevada a la segunda potencia. Sin embargo, cuando se escribe en la forma más simple juntando los términos iguales, los dos términos x2 desaparecen y la ecuación se reduce a 4x = 28. Por tanto, esta ecuación es de primer grado.
Ya hemos aprendido a resolver ecuaciones de primer grado sumando, restando, multiplicando o dividiendo ambos miembros de la ecuación por el mismo número. En estas páginas seguiremos aplicando estos métodos para resolver ecuaciones; sin embargo, ahora resolveremos ecuaciones que pueden contener tanto números negativos como positivos. Además, aprenderemos algunos “atajos” que nos facilitarán el trabajo.
Enunciemos una vez más los cuatro principios que hemos aplicado en la resolución de ecuaciones. Estos principios se aplican tanto a las ecuaciones que contienen números negativos como a las que contienen números positivos. Estos principios se denominan axiomas. Un axioma es una afirmación que se acepta sin pruebas.
