
Calculadora de ecuaciones dimensionales
Aunque no sepa qué es el análisis dimensional y para qué se utiliza, ¡no se preocupe! Nosotros también lo sabemos. Sigue leyendo este artículo para conocer la definición de análisis dimensional y los ejemplos de su aplicación. También aprenderá a realizar el análisis dimensional para convertir de un sistema de unidades a otro.
El análisis dimensional (o análisis de unidades) es un método en el que analizamos las cantidades físicas en términos de sus unidades o dimensiones. Mediante este proceso, podemos convertir entre diferentes unidades de una magnitud física. Para ello, necesitamos encontrar el factor de conversión, que se puede multiplicar por la medida en un sistema de unidades para convertirla a otros sistemas de unidades.
Para expresar el valor de las cantidades físicas, es necesaria una unidad. Si no, ¿cómo podríamos decirle al tendero cuánto azúcar, harina, aceite, etc., necesitamos? Sin embargo, el número de magnitudes físicas que medimos es enorme. Imagínate lo difícil que nos resultaría recordarlas todas si tuviéramos que definir una unidad distinta para cada una.
Calculadora de ecuaciones dimensionales
La adimensionalización es la eliminación parcial o total de las dimensiones físicas de una ecuación en la que intervienen cantidades físicas mediante una sustitución adecuada de las variables. Esta técnica puede simplificar y parametrizar problemas en los que intervienen unidades de medida.
La calculadora de densidad no dimensional utiliza Densidad no dimensionalizada = Densidad/Densidad del líquido para calcular la Densidad no dimensionalizada, La fórmula de la densidad no dimensional se define como la relación entre la densidad y la densidad de la corriente libre del líquido
¿Cómo se calcula la densidad adimensional con esta calculadora en línea? Para utilizar esta calculadora online para la densidad adimensional, introduzca la densidad (ρ) y la densidad del líquido (LD) y pulse el botón de calcular. Así es como se puede explicar el cálculo de la densidad adimensional con los valores de entrada dados -> 99.7 = 997/10.
Asumiendo un flujo constante y se representa como ρ- = ρ/LD o Densidad No Dimensionada = Densidad/Densidad del Líquido. La Densidad de un material muestra la densidad de ese material en un área específica dada. Se toma como masa por unidad de volumen de un objeto dado y la Densidad del Líquido es la masa por unidad de volumen del líquido.¿Cómo calcular la Densidad No Dimensionada? La fórmula de la Densidad No Dimensionada se define como la relación entre la densidad y la densidad de la corriente libre del líquido
Ecuaciones dimensionalmente correctas
Una esfera es la contrapartida tridimensional de un círculo bidimensional. Es un objeto geométrico perfectamente redondo que, matemáticamente, es el conjunto de puntos que equidistan de un punto dado en su centro, donde la distancia entre el centro y cualquier punto de la esfera es el radio r. Probablemente el objeto esférico más conocido es una bola perfectamente redonda. En matemáticas, se distingue entre una bola y una esfera, donde una bola comprende el espacio delimitado por una esfera. Independientemente de esta distinción, una bola y una esfera comparten el mismo radio, centro y diámetro, y el cálculo de sus volúmenes es el mismo. Al igual que en el caso de un círculo, el segmento de línea más largo que une dos puntos de una esfera a través de su centro se denomina diámetro, d. A continuación se proporciona la ecuación para calcular el volumen de una esfera:
EJEMPLO: Claire quiere llenar de vinagre un globo de agua perfectamente esférico con un radio de 0,15 pies para utilizarlo en la pelea de globos de agua contra su archienemiga Hilda este próximo fin de semana. El volumen de vinagre necesario puede calcularse utilizando la ecuación que se proporciona a continuación:
Calculadora de análisis dimensional moles
La dimensión de una magnitud física se define como la potencia a la que se elevan las magnitudes fundamentales para expresar la magnitud física. Por ejemplo, la dimensión de la velocidad es 0, 1, -1 en Masa, Longitud, Tiempo, respectivamente.
Nota: Podemos calcular la fórmula de la dimensión de una magnitud física cuando se conoce su relación con otras magnitudes físicas. En nuestros ejemplos, podemos calcular la fórmula dimensional de la densidad una vez que sabemos cómo se relaciona con la masa y el volumen.
Cantidad físicaFórmula dimensional
UnidadSIÁrea[ M0 L2 T0 ]m2Volumen[ M0 L3 T0 ]m3Velocidad[ M0 L1 T-1 ]ms-1Aceleración[ M0 L1 T-2 ]ms-2Momentum[ M1 L1 T- 1 ]kg m s-1Fuerza[ M1 L1 T-2 ]kg m s-2Presión[ M1 L-1 T-2 ]kg m-1 s-2Trabajo/Energía[ M1 L2 T-2 ]kg m2 s-2Potencia[ M1 L2 T-3 ]kg m2 s-3Constante gravitatoria[ M- 1 L3 T-2 ]kg-1 m3 s-2Impulso[ M1 L1 T-1 ]kg m s-1Tensión superficial[ M1 L0 T-2 ]kg s-2Coeficiente de viscosidad[ M1 L-1 T-1 ]kg m-1 s- 1Momento de inercia[ M1 L2 T0 ]kg m2Momento angular[ M1 L2 T-1 ]kg m2 s-1Torque/par[ M1 L2 T-2 ]kg m2 s-2Frecuencia[ M0 L0 T-1 ]s-1Fórmula dimensional de diferentes magnitudes físicas
Conclusión
Ecuación dimensional es aquella igualdad matemática que sirve para relacionar las magnitudes derivadas en función de las fundamentales.
En su forma general, una ecuación dimensional se escribe de la siguiente manera:
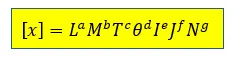

También te puede interesar:
Ecuación de una circunferencia
